-
チラシの純粋な効果を推量する事例について
2021.06.30
-
 詳細を次頁以降で説明します。
詳細を次頁以降で説明します。【課題提起】
下記の表1は、ある店舗で行った折り込みチラシの広告効果調査結果である。 この結果から、当店が実施した折り込みチラシの効果は、どれ位あると考えたらよいのか?

上記が、折り込みチラシの広告効果測定にあたり設定したアンケート質問項目である。
【チラシの広告効果をどう捉えるか】
もちろん、これ以外にも回答者の属性等に関する質問をいくつか設定したが、広告効果を検証するに あたっては、前頁2つの質問で十分である。では、その分析方法とはどのようなものであろうか?
以下、これについて説明する。
表2を参照頂きたい。これは 「チラシの認知状況」 と 「チラシ掲載目玉商品の購入状況」 のクロス 集計の概要を示したものである 。
下記 a~f のうち、実際に調べなければいけないのは a~d である。 e=a+b であるし、f=c+d である。
このように、効果算出にあたって設定するデータはきわめてシンプルである。
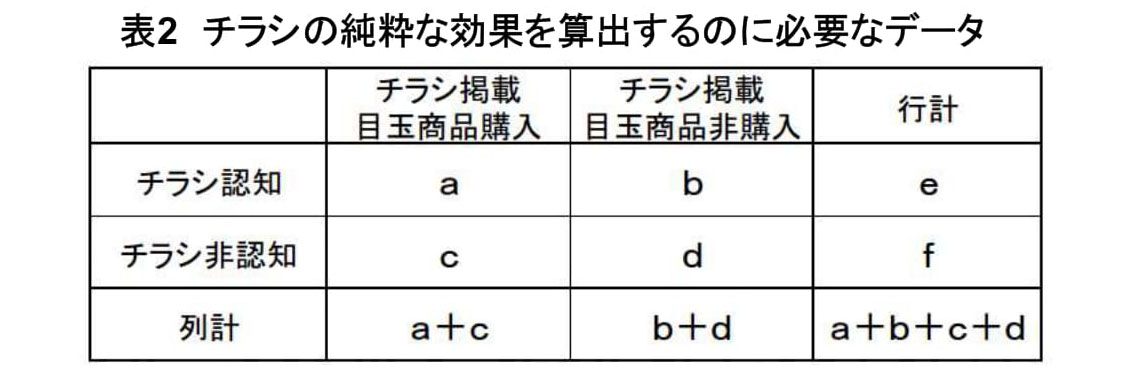
もう一度、表2をじっくり見て頂きたい。このうち 「a+c」 は何を意味するか?
もちろん、それはチラシ掲載目玉商品を購入した人の合計数である。
同様にして 「b+d」 は、チラシ掲載目玉商品を購入しなかった人の合計数である。では 「e」 は何を意味するか?
それは、チラシを見た人の合計人数である。同様に、「f」 はチラシを見なかった人の合計数である。さて、ここからが本丸である。
「チラシを見て、かつ、目玉商品を購入した人」 の数は 「a」 であるが、この 「a」 のうち 「チラシを見た 影響を受けて目玉商品を購入した人」 はどれだけいると考えられるか?
話がちょっとややこしくなってきたが、整理して考えれば、それ程むずかしくない。
「a」 という数の中には、 「チラシを見て、その影響を受けて目玉商品を購入した人の数」 と、 「チラシを見ていなかったとしても、目玉商品を購入した人の数」 の、2つの数が含まれているのだ。
これらのうち、前者がチラシ広告によって純粋に生み出された需要。つまり、創出された需要という わけだ。これが本当の意味でのチラシ効果と言える。
問題は、このチラシ広告で創出された数をどうやって割り出すかである。
くどいようだが、もう一度、表2をじっくり見てもらうとこの方法がわかる。 気づかれた方もいると思うが、それは次の数式で算出できる。
そう、「a」、「c」、「e」、「f」 の4つの数値の関係に注目すればよいのである。
つまり、「a」 の中に、たとえチラシを見ていなくても目玉商品を購入した人がいるとすれば、
それは 「チラシを見ずに、目玉商品を購入した人」 の割合と同じだけいると考えるのが妥当であろう。 チラシの認知条件以外は、少なくとも同じエリア、タイミング、方法で得られたデータだからである。上記の割合を 「c」、「f」 を使って表せば、次のとおりである。
チラシを見ずに目玉商品を購入した人の割合= c/f ・・・・・・・・・・・1
したがって、「チラシを見て目玉商品を購入した人」 の中で、「チラシを見なかったとしても目玉商品を 購入したと考えられる人」 の数は、次のとおりである。
実際はチラシを見て目玉商品を購入したが、そのうち チラシを見なかったとしても購入したと考えられる人の数
= e × c/f ・・・・・2よって、「チラシを見たために目玉商品を購入した」 という、チラシの効果に触発されて購買に至った人数は、
a-(e×c/f) である。以上のことを整理すると、チラシにより創出された購買行動の寄与率は次の式で表せる。
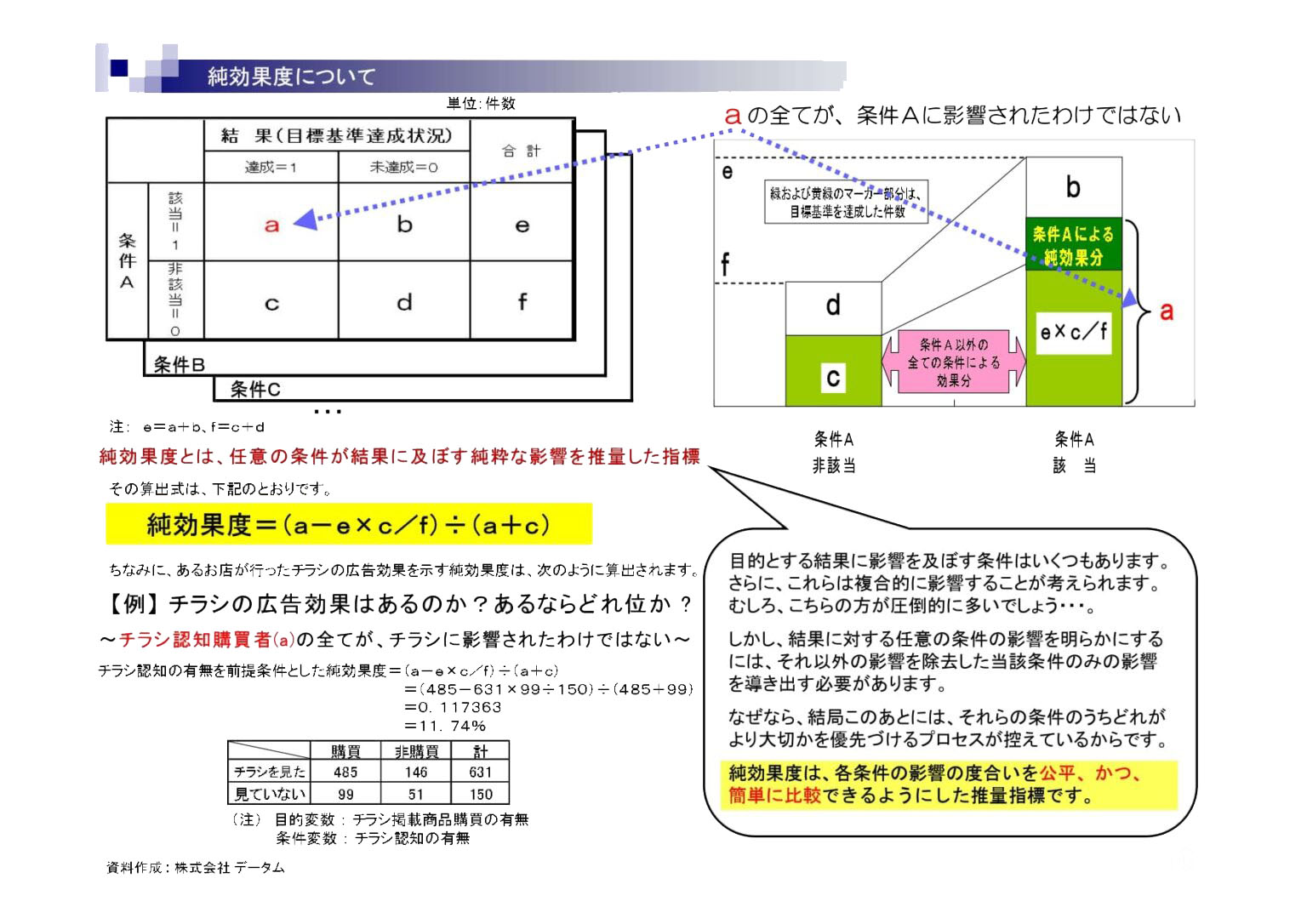
チラシにより創出された購買行動の寄与率={a-(e×c/f)}/(a+c)・・・・・・・3
この3の比率が 「純効果度」 である。いわば、施策(当事例ではチラシ)の純粋な効果と言える指標 である。
ここでちょっと話がそれるが、上記3式にはデータの意味を読む際のポイントが潜んでいるので、 これについても触れておきたい。
それは、任意条件の有無による、結果の違いを検証する際の根幹に関わることである。 お気づきの方もいると思うが、具体的には 「-(e×c/f)」 の部分である。
これは「実際はチラシを見て目玉商品を購入したが、そのうち、チラシを 見ていなくても購入したと考えられる数」 を差し引くことを意味する。
もう一歩踏み込んで考えると、これは次のようなデータ処理をしていることに相当する。
「任意条件の影響を比較できるようにするための、公平な前提(共通土俵)の設定」 である。 目玉商品購入に影響を及ぼすのは、何もチラシ認知の有無だけではない。他にもさまざまな要因が影響していると考える方が、むしろ自然である。
このことを承知した上で、チラシの認知いかんによる結果の違いをクローズアップするには何が 必要か?
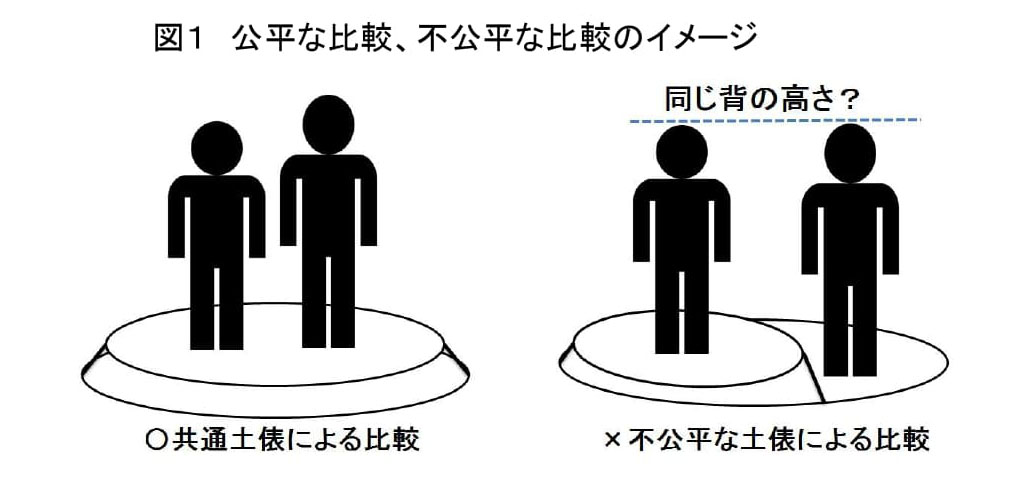
そう、それはチラシ認知以外の一切の影響を、チラシ認知購買者数から取り除くことである。 こうすることで初めて、同じ土俵でチラシ認知の有無による結果を公平に比較でき、意味があるからだ。
そしてこれを実現するのが、上述した 「-(e×c/f)」 という割り戻し項目である。
じつは、これは統計学でいうところの 「偏」 という考え方である。偏とは、ある特定の条件の影響を見る ときは、それ以外の条件の影響を固定しておくという考えである。偏回帰係数、標準偏回帰係数、偏相関 といった言葉を思い出された方もいるだろう。
「純効果度」 は、この「偏」 なる考えを最もシンプルな形で示した指標であると、筆者は考えている。 考えてみれば、世の中の現象は様々な要因が複雑に組み合わさった結果であることが多い。
しかしこうした場合でも、純効果度の考え方、すなわち偏なる考え方を用いれば、任意条件の純粋な 影響度を推し量ることができる。シンプルだけど、とても役立つ指標である。
一般的に任意条件の影響力や効果を検討する場合、統計学における 「ランダム比較テスト」 が有効である。
しかし、ラボにおける実験と違い、社会経済的な事象の場合、テストの前提条件を厳密に制御する こと自体難しいのが現実である。こうした点を踏まえて考案した推量指標が、「純効果度」 である。
さて、以上の予備知識を頭にとどめた上で、再び話をもとにもどそう。
チラシの純効果度は11.7%。つまり、販売された商品のうち11.7%がチラシの需要創出効果により 生み出されたものと推量できる。
一方、よくある勘違いは、チラシ認知購買者(a=485)÷チラシ認知者(e=631)×100=76.9%、 この比率をチラシの効果と判断することだ。
もしこんなに効果があるなら、それこそ湯水のようにチラシを撒きたくならないだろうか・・・?
でも現実問題、そんなに上手い話しはあり得ない。以上、当事例ではチラシの広告効果のテーマを題材に、 「純効果度」 というシンプルな効果測定法を 紹介した。
純効果度は当事例でとりあげた広告効果だけにとどまらず、任意の対策が目的とする対象にどれ位 の影響を及ぼすかというテーマ全般について有効である。
算出式も非常にシンプルであるから、実務的にも利用価値が高いと考えられる。読者の皆さまも、 身近にあるデータで試して頂ければ幸いである。
当資料を最後までご覧頂き、ありがとうございました。
ご不明な点やご質問は下記までお願いします。
ご紹介した純効果度ですが、当尺度にはもうひとつ面白い特徴があります。
それは、 「影響のベクトル指標」 です。通常の相関とは違い、任意の2項目
間の影響の方向や度合いを推察できます。
この特徴を活かした分析事例をご希望の方には、概要資料をお送りいたしま
す。下記メール宛に資料請求してください。〒 101-0034
東京都千代田区神田東紺屋町30番地 サンハイツ神田ビル8F
株式会社データム 担当:舘野
電話: 03-3255-6851 電子メール:info@dtum.co.jp
